123do: Creation of a cube with and without collision box
One-Two-3DO (also known as 123do)
One-Two-3DO or in short 123do let's you create 3DO objects for GPL. You can get it here: [Link to One-Two-3DO].
It runs fine here for me with Windows Vista 64 bit with an Nvidia 8800GTS. Only thing which had to be changed is to "Disable desktop composition for the OneTwo3DO.exe like you can see in this screenshot
If you start it you will see a window like this:
Now you must understand that you need points (vertics) to attach polygons and lines on them.
Let's create a simple 3DO cube.
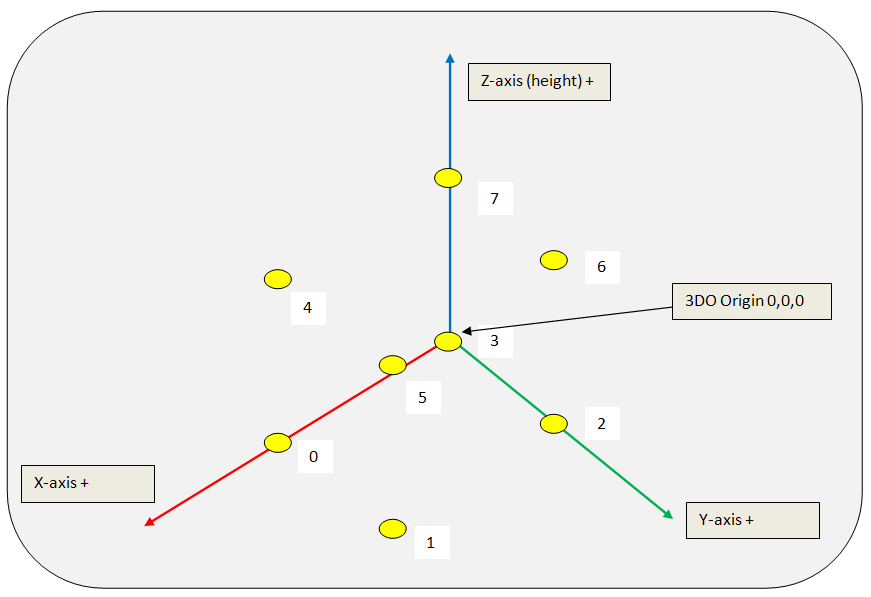
First, here's a picture of the 3D room and how the vertics are positioned for a cube.
I have numbered the vertics we need for a cube from 0 to 7.
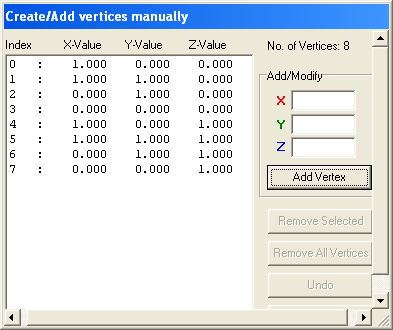
If I want to create a 3DO with a dimension of 1 unit for every side of the cube I would create those 8 vertics:
vertics index x y z
0 1 0 0 1 1 1 0 2 0 1 0 3 0 0 0 4 1 0 1 5 1 1 1 6 0 1 1 7 0 0 1
You need those vertics as points for polygons or lines. Without those vertics you can not assign a polygon or a line to it.
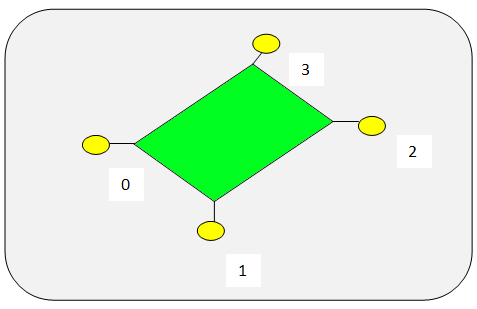
Here's a picture to display an idea how it works for a simple polygon:
The edges of the polygon are attached to the vertics.
Now this should be enough for the basics of vertics and polygons.
To add the vertics to 123do open the Create/Add vertices manually from here:
You should then see this window:
I have filled in the values of vertic 0. Finished it looks like this:
Close the dialog and choose File/Save project. Make it easy and give it the name of the 3DO. Please use 8.3 syntax naming the project. Now we come to the hardest part of it. We need to add the polygons. When adding the polygons, the sequenz how you add the vertics will be critical from where your polygon will display an attached texture (bmp in 123do and as a mip in GPL).
If we add the vertices 0,1,2,3 in that sequenz you can see from the picture above that this is the bottom of the cube. Imagine watching from the bottom:
0,1,2,3 would be clockwise. This would result in a plane pointing in your direction which would mean that you can see the image. 3,2,1,0 would be anti-clockwise. This would result in a plane pointing away from you which would mean that you can't see the image.
Please select the Create Polygons button:
I have filled in the values for this polygon as well as the values for the remaining 5 polygons.